原子　atom


光子のエネルギー
真空中において、金属の固体表面に光を照射したとき、その金属表面から電子が 放出される現象のこと光電効果をいう。 このとき放出される電子の運動エネルギーは、照射する光の強さには依存せず、 照射する光の振動数 ν (ニュー) に比例して変化する。 この現象は古典物理学における光の波動論によって説明することが難しく、 結局 光がエネルギー
　　　E ＝ h ν
をもつ粒子のように振舞うことが示された。 これは歴史的には光量子説とも呼ばれ、 1905年に A．Einstein (アインシュタイン) によって提唱された。 このような光の粒子のことを光子という。 ここで h は プランク (Planck)定数と呼ばれる基本定数であって、 およそ
　　　h ≒ 6.6×10⁻³⁴　J・s
である。
［注］単位 J・s の呼称は 「ジュール・秒」。
すなわち 光の振動数が大きいほど、光子１個あたりのもつ運動エネルギーは大きくなる。 プランク定数は、1900年に M．Planck が エネルギー量子説を提唱した際に導入した重要な基本定数である。
真空中の光速度を c とし、光の波長を λ (ラムダ) とするとき、光の波動論によれば
　　　c ＝ ν λ
の関係があるので、光子のエネルギー E は
　　　E ＝ h c／λ
とも記せる。 ただし 真空中の光速度 c は およそ
　　　c ≒ 3×10⁸ m/s
であって、重要な基本定数である。 このように光は波動であると同時に粒子の性質をも併せ持っている。 この事は、現代物理学の基礎理論である量子論 (quantum theory) によって 説明される。
一般に量子論的に考えると、電子や光子のような素粒子に属する 微視的(ミクロ)対象は、粒子性と波動性を併せもっており、そのときの物理的状況に応じて何れかの性質が顕著に現れる。 ここで素粒子とは、物質を構成する要素の中で最小単位に属する粒子のことをいう。 一般に原子レベル以下の微視的(ミクロ)対象は、ニュートン力学のような古典物理学の 範囲内で理解することは困難であって、量子論に基づいて考察する必要がある。 古典物理学は、一般に巨視的(マクロ)対象に対して適用される。

原子模型
水素原子 H は、その中心にある１個の陽子 ｐ からなる核の周囲を、１個の電子 ｅ が 周回している系であって、周期表中にある元素の内で最も単純な構造をもつ原子である。 N．Bohr (ボーア) の水素原子模型は歴史的によく知られている。 原子のほぼ中心に存在する核のことを原子核または核と呼ぶ。 核の構成要素である陽子 ｐ は、正電気量　約 1.60×10⁻¹⁹ C (クーロン) をもち、 質量は約 1.67×10⁻²⁷ kg の素粒子である。 一方の電子 ｅ は、陽子 ｐ と反対の負電気量をもち、質量は約 9.11×10⁻³¹ kg の 素粒子である。 一般に原子は、原子核と電子の間に作用している静電引力によって構成される。 この静電引力の強さは、電磁気学で知られているクーロンの法則に従う。 原子の直径は およそ 10⁻¹⁰ m のオーダーであるが、原子核の直径は遥かに小さく、 およそ 10⁻¹⁵ m のオーダーである。 元素の周期表上の原子番号は、その原子核に含まれる陽子 ｐ の個数に等しい。 通常の原子では、核の周りを廻る電子 ｅ の個数は陽子 ｐ の個数に等しく、 原子全体としては正負の電気量が互いに相殺して電気的に中性の状態となっている。 電子 ｅ の質量は、陽子 ｐ の質量の約 1800分の 1 であって極めて軽いために、 原子の質量の大部分は原子核が占めている。 水素原子以外の核では、陽子 ｐ の他に中性子と呼ばれる素粒子も含んでいる。 中性子は陽子 ｐ の質量とほぼ等しいが、電気を帯びていない素粒子である。 （厳密には中性子の質量の方が陽子の質量よりもわずかに大きい。）

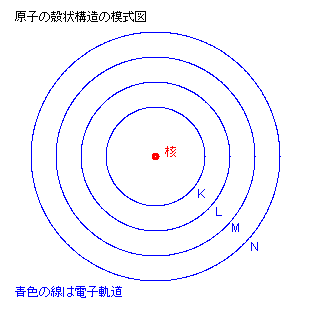
原子の殻状構造
原子内の電子は、核の周囲の定められた軌道上を周回運動している。 核に最も近い内側の電子軌道は K 殻と呼ばれエネルギーが最も低く、 そこに居る電子は極めて安定な状態にある。 この K 殻の軌道には、電子が 2 個までしか入り得ない。 その外側の電子軌道は L 殻と呼ばれ、電子が 8 個まで入ることが出来る。 さらにその外側には M 殻と呼ばれる軌道が存在し、そこには 18 個までの電子が入り得る。 一般に外側の周回軌道ほどエネルギーが高く、そこに居る電子は不安定であるために、 原子内の電子は安定な内側のエネルギーの低い軌道に遷移する傾向がある。 このように原子内の電子は内側の殻から順に　K， L， M， N， などの順に占有されていく。 それぞれの軌道は主量子数 n をもっており、 K 殻では　n ＝ 1，　L 殻は　n ＝ 2，　M 殻は　n ＝ 3，　 N 殻は　n ＝ 4　などと順に整数値が付与されている。 このとき 各軌道に入り得る電子の個数 N の上限は、次式によって与えられる。
　　　N ＝ 2n²
したがって　それぞれの殻に入り得る電子の個数は次の表のようになる。

原子の種類	原子番号	K 殻	L 殻	M 殻	N 殻
水素 H	1	1	0	0	0
ヘリウム He	2	2	0	0	0
リチウム Li	3	2	1	0	0
ベリリウム Be	4	2	2	0	0
ほう素 B	5	2	3	0	0
炭素 C	6	2	4	0	0
窒素 N	7	2	5	0	0
酸素 O	8	2	6	0	0
フッ素 F	9	2	7	0	0
ネオン Ne	10	2	8	0	0
ナトリウム Na	11	2	8	1	0
マグネシウム Mg	12	2	8	2	0

　
原子内の電子が低いエネルギー軌道上にあるとき、 その原子は基底状態にあるといい、安定である。 原子内の電子が外側の高いエネルギー軌道上に遷移したとき、 その原子は励起状態にあるといい、不安定である。 励起状態にある原子内の電子は、安定な電子配置を得ようとして エネルギーの低い内側の軌道に遷移する。 この際に電子は余分なエネルギーを 電磁波 (光 や X 線など) の形で放射して、 原子自身は安定な基底状態となる。 高いエネルギー E_２ の軌道にあった電子が 低いエネルギー E_１ の軌道に遷移したとき 放射される電磁波 (光や X 線など) の振動数 ν (ニュー) は、 一般に次式によって与えられる。
　　　h ν ＝ E_２−E_１
ここで　h ν　は放射される光子１個あたりのエネルギーである。
量子論によると、電子は波動的性質を併せ持っているために、 原子内のような微視的領域において、 電子の描く軌道を明確に記述することは困難であって、 各点における電子の存在確率の密度分布が把握される。 歴史的には、量子論における確率解釈はコペンハーゲン派の量子論研究者によって 20世紀初頭に提唱された。 （この量子論の確率解釈については、その後も様々な議論がされている。）
したがって上記の原子の殻状構造の図は、あくまでも模式図であって、 実際の電子の描く軌道を厳密に図に記すことは難しい。 各点における電子の存在確率密度を規定する法則は、 シュレディンガー方程式と呼ばれる微分方程式によって表現され、 これは量子論における基本方程式の一つであって低エネルギー領域の電子の挙動を 解明する際に適用される。
電子はスピンと呼ばれる量子数が 1／2 の値をもつ素粒子であって、フェルミ粒子に属する。 ここでフェルミ粒子とは、スピン量子数が半奇数の値をもつ素粒子の総称である。 一般にフェルミ粒子は物質を構成する素粒子である。 フェルミ粒子は同一の物理的状態に複数個の粒子が入ることができず、一つの状態には 必ず一個の粒子しか入り得ないという性質がある。 電子がもつフェルミ粒子としての性質が基因となって、原子の殻状構造が形成される。 これに対して光子はスピン量子数が 1 であって、ボース粒子に属する素粒子である。 ここでボース粒子とは、スピン量子数が整数の値をもつ素粒子の総称である。 一般にボース粒子は力を媒介する素粒子である。 ボース粒子は同一の物理的状態に複数個の粒子が入り得る。

原子の電離
原子が光の照射を受けると原子内の電子は光のエネルギーを吸収して、 外側のエネルギーの高い軌道に遷移するために原子は励起状態となる。 振動数 ν (ニュー) の光について、 その光子のエネルギー E は振動数 ν に比例し、
　　　E ＝ h ν
で与えられる。 ただし h はプランク定数である。 したがって 紫外線のように振動数 ν の大きい光は、 光子 １個あたりのエネルギー E が大きい。 原子内の電子が光子のエネルギー h ν を受けて、 低いエネルギー E_１ の軌道から エネルギーの高い E_２ の 軌道へ遷移するとき、一般に次式が成り立つ。
　　　h ν ＝ E_２−E_１
特に振動数の極めて大きな光を照射された場合には、 その原子は大きなエネルギーを光から受けるので、 原子内の電子は軌道から完全に離脱し、 その原子は １個または幾つかの電子を失うことがある。 原子がこのような状態になることを 電離 または イオン化 という。 原子内から １個の電子を離脱させるために要する最小のエネルギーを 電離エネルギー または イオン化エネルギーという。

原子内の電子配置
原子内における電子の周回軌道は、それぞれの殻 K， L， M， N などの中で更に 細分化されており、s， p， d， f　などの名称で呼ばれ、それぞれの名称の前には 主量子数 n の値を付して記される。
　K 殻　( n ＝ 1 )　：　1s
　L 殻　( n ＝ 2 )　：　2s， 　2p
　M 殻　( n ＝ 3 )　：　3s， 　3p， 　3d
　N 殻　( n ＝ 4 )　：　4s， 　4p， 　4d， 　4f
上記に示されているようにエネルギーの最も低い内側の K 殻では s 軌道が一つ存在するだけであるが、外側の殻になると p 軌道や d 軌道など複数個の軌道が存在する。 それぞれの細分化された軌道上に入り得る電子の個数の上限は、 次のように定まっている。
　s 軌道　：　2 個
　p 軌道　：　6 個
　d 軌道　：　10 個
　f 軌道　：　14 個
一般に 主量子数 n の各 s，p，d，f　等の軌道に配置されている電子の個数を m とするとき
　( n s )^m，　( n p )^m，　 ( n d )^m，　( n f )^m
などのように記して原子内の電子配置を表す。

［ 電子配置の例 ］

原子の種類	原子番号	K 殻	L 殻	M 殻	N 殻
水素 H	1	(1 s)1
ヘリウム He	2	(1 s)2
リチウム Li	3	(1 s)2	(2 s)1
ベリリウム Be	4	(1 s)2	(2 s)2
ほう素 B	5	(1 s)2	(2 s)2 (2 p)1
炭素 C	6	(1 s)2	(2 s)2 (2 p)2
窒素 N	7	(1 s)2	(2 s)2 (2 p)3
酸素 O	8	(1 s)2	(2 s)2 (2 p)4
フッ素 F	9	(1 s)2	(2 s)2 (2 p)5
ネオン Ne	10	(1 s)2	(2 s)2 (2 p)6
ナトリウム Na	11	(1 s)2	(2 s)2 (2 p)6	(3 s)1
マグネシウム Mg	12	(1 s)2	(2 s)2 (2 p)6	(3 s)2
アルミニウム Al	13	(1 s)2	(2 s)2 (2 p)6	(3 s)2 (3 p)1
シリコン Si	14	(1 s)2	(2 s)2 (2 p)6	(3 s)2 (3 p)2
りん P	15	(1 s)2	(2 s)2 (2 p)6	(3 s)2 (3 p)3
硫黄 S	16	(1 s)2	(2 s)2 (2 p)6	(3 s)2 (3 p)4
塩素 Cl	17	(1 s)2	(2 s)2 (2 p)6	(3 s)2 (3 p)5
アルゴン Ar	18	(1 s)2	(2 s)2 (2 p)6	(3 s)2 (3 p)6
カリウム K	19	(1 s)2	(2 s)2 (2 p)6	(3 s)2 (3 p)6	(4 s)1
カルシウム Ca	20	(1 s)2	(2 s)2 (2 p)6	(3 s)2 (3 p)6	(4 s)2
スカンジウム Sc	21	(1 s)2	(2 s)2 (2 p)6	(3 s)2 (3 p)6 (3 d)1	(4 s)2
チタン Ti	22	(1 s)2	(2 s)2 (2 p)6	(3 s)2 (3 p)6 (3 d)2	(4 s)2

最も外側の殻内において、電子が未占有状態の軌道があると、その原子は外部から電子を 取り込んで軌道を満たそうとする傾向がある。 したがって電子が未占有の最外殻軌道をもつ原子は、他の原子と結合するなどの 化学的反応性に富んでいる。 最外殻内の軌道が電子で満たされているときは、化学的に安定であって、いわゆる 不活性元素となる。 一般に化学反応現象は、原子内の最外殻軌道上にある電子の挙動に帰着される。
量子論によると、s 軌道にある電子の存在確率密度の分布は球対称であるが、 p 軌道や d 軌道などについては、特定の方向に突出した存在確率の密度分布をしている。

Ｘ線
Ｘ線は波長が 10⁻⁹ 〜 10⁻⁶ cm 程度の電磁波 (光子) であり、 1895年に W．Roentgen (レントゲン) によって発見された。 Ｘ線は波長が短いほど物質に対する透過性が強くなり、 短波長側は γ (ガンマ)線に移行する。 また 長波長側では紫外線に移行する。 Ｘ線を発生させる真空管を Ｘ線管という。 Ｘ線管は、真空にしたガラス管内に陰極と陽極ターゲットが封入されており、 これに高電圧を印加して使用する。 ターゲット物質は重金属 (タングステン，鉄，銅など) で作られている。 一般に 真空中において電子を高電圧（10⁴ V 〜10⁵ V ）で 加速して ターゲットに衝突させると Ｘ線が放射される。 Ｘ線管に印加される電圧を V [V ボルト]，電流を i [A アンペア]， ターゲット金属の原子番号 Z とすると、単位時間あたりに放射される Ｘ線の全エネルギー P [W ワット] は
　　　P ＝ η Z i V ²
で与えられる。 ただし η (イータ) は 定数で S I 単位系では 10⁻⁹ V⁻¹ となる。 Ｘ線管に供給される電気エネルギーの大部分は、熱エネルギーとなって外系へ 散逸し、ごく一部が Ｘ線のエネルギーに変換されるにすぎない。

［例題１］
Ｘ線管に印加する電圧と管電流が定められているとき、ターゲットの金属を 銅からタングステンに変更すると、放射されるＸ線のエネルギーは幾倍となるか。 ただし 銅 Cu，タングステン W の原子番号をそれぞれ 29，74 とする。
（解）
　P ＝ η Z i V ²　　より
　P_Cu＝ 29 η i V ² ，
　P_W＝ 74 η i V ²
　よって　P_W／P_Cu ＝ 74／29 ＝ 2.55 倍

［例題２］
Ｘ線管のターゲット金属や管電流が定められているとき、Ｘ線の 放射エネルギーを 2倍にするためには管電圧を幾倍にすればよいか。
（解）
　P ＝ η Z i V ²　　より　
　P ＝ η Z i E₁² ，　
　2P ＝ η Z i E₂²
　したがって
　2P／E₂² ＝ P／E₁²
　E₂ ＝ √2 E₁
　よって　√2 倍

連続Ｘ線 と 特性Ｘ線
連続Ｘ線とは、陽極ターゲットの物質に関係なく連続スペクトルをもつＸ線のことをいう。 連続Ｘ線は、高速な電子がターゲットに衝突する際に、電子の制動放射によって生ずる。 ここで 制動放射とは電子が減速される際に、電子のもつ運動エネルギーの一部が 電磁波 (Ｘ線など) のエネルギーに変換されて放射されることをいう。 これに対して、特性Ｘ線とは 陽極ターゲットの物質に固有の線スペクトルをもつＸ線のことをいう。 特性Ｘ線は、電子が高速でターゲットに衝突したときに、ターゲット物質の原子が励起 されることにより生ずる。
［注］透過性の強いＸ線 (短波長) を硬Ｘ線、透過性の弱いＸ線 (長波長) を軟Ｘ線と言うことがある。

Ｘ線の散乱
Ｘ線は電子などの荷電粒子に当たると散乱される。 Ｘ線の散乱にはThomson (トムソン)散乱とCompton (コンプトン)散乱がある。 Thomson 散乱は電子が入射 線 (電磁波) を受けて振動を起こすことにより生ずる。 Thomson 散乱では散乱Ｘ線の波長は入射Ｘ線の波長に等しい。 Compton 散乱は入射Ｘ線 (光子) が電子と衝突する際、光子のもつ運動量と エネルギーの一部を電子に与えることにより生ずる。 Compton 散乱では散乱Ｘ線の波長は入射Ｘ線の波長と異なっている。

Ｘ線の吸収
Ｘ線が物質中を通過するとき、物質に吸収されてＸ線強度は指数関数的に減衰していく。 初め強度 I₀ のＸ線が、厚さ x の一様な物質中を通過すると、 その強度 I は
　　　I ＝ I₀ e^{−μ x}
となる。 ここで μ (ミュー) を線吸収係数といい、 入射Ｘ線の波長で決まる定数である。

　

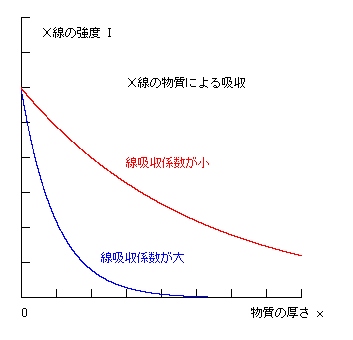
上図においては 横軸ならびに縦軸とも任意スケールであって、全体の傾向のみを示す。
単体物質においては、その物質の密度 ρ (ロー) としたとき　μ／ρ　の ことを質量吸収係数という。 質量吸収係数は物質の凝集状態に依存しない定数となる。

［例題３］
定められた強度のＸ線を均一な物質中に入射させたとき、表面より深さ 30.0 mm の点での 強度が表面の 1／2 になった。 このとき表面の強度の 1／10 になるような深さを求めよ。
（解）
　I ＝ I₀ e^{−μ x}　　より
　I／( 2 I ) ＝ e^{−30.0 μ}　，
　I／( 10 I ) ＝ e^{−x μ}
　したがって
　μ ＝ (log_e2)／(30.0 mm)　
　x ＝ (log_e10)／μ　
　よって
　x ＝ 30.0 (log_e10)／(log_e2) mm
　　＝ 99.7 mm

原子の結合
分子は原子が結合して構成され、それ自体が一個の独立粒子として振舞う。 気体の場合、各分子は互いに独立に自由に運動しており、 常温のときの気体分子運動の平均速度は 約 10² m/s から 10³ m/s の程度である。 したがって気体の状態において物質は定まった形や体積をもたず、拡散する性質をもつ。 物質は高温並びに低圧の環境において気体となる傾向がある。
　[例]　水素分子 H₂ ， 　酸素分子 O₂ ， 　窒素分子 N₂　など。
固体は、莫大な数の原子が結合して、格子状に規則的に配列して構成される。 このような原子の規則的配列のことを、結晶構造という。 固体を構成する各原子の位置は定まっており、自由に運動することはできないが、 各位置で振動する程度の動きは可能である。 物質は低温並びに高圧の環境では固体となる傾向がある。
　[例]　塩化ナトリウム NaCl ， 　ダイヤモンド C ， 　シリコン Si　など。
分子同士が互いに弱く結合して構成される結晶は分子結晶と呼ばれ、 多くの有機化合物の結晶はこれに属する。 一般に分子結晶は融点が低く、更に蒸発や昇華しやすいが、 分子量の大きい有機高分子結晶の場合は安定な固体となる。
　[例]　ナフタリン ，　ベンゼン　など。
原子の配列が規則的でない場合には非晶質 (アモルファス) と呼ばれる。 液体の場合、各原子や分子の相互の位置が、たえず変化している。 したがって液体状態の物質は一定の体積を保つが、定まった形をもたない。 ガラス状態は非晶質の一種であって、極めて高い粘性係数の液体とみなせる。

原子の結合には最外殻軌道に存在する電子が関与している。 水素原子 H では、最外殻の K殻の軌道にある電子が結合に関与して、 水素分子 H₂ が構成される。 酸素原子 O では、最外殻の L殻の軌道にある電子が結合に関与して、 酸素分子 O₂ が構成される。

　

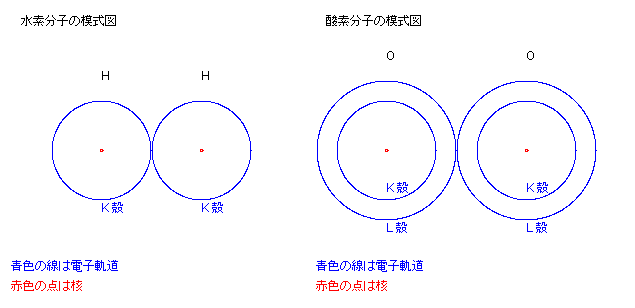
なお 量子論によると、電子は波動的性質をもっているので、 原子内の電子軌道を明確に描くことは困難である。 したがって上記の二原子分子の図は、あくまでも模式図である。 量子論的には、原子内の各点における電子の存在確率の密度分布が把握される。

結合の状態
一般に原子の結合状態は次のように分類される。 原子が結合して分子や固体が形成されるとき、以下の各結合状態が複合的に関与している場合が多い。

（共有結合）
二つの原子が軌道電子を互い一個づつ対で共有して最外殻の軌道を満たし、 安定な電子対を構成することによって生ずる。 一般に二原子分子のような同種類の原子同士は、共有結合する傾向がある。 更に有機化合物の分子には共有結合によって構成されるものが数多く存在する。
　[例]　水素分子 H₂ ， 　酸素分子 O₂ ，　メタン CH₄ ，　エタン C₂H₆　など。
共有結合によって構成される固体は共有結晶と呼ばる。 共有結晶は、硬度や融点が高く且つ化学的にも安定であり、熱膨張係数が小さい。 また共有結晶は常温において電気の絶縁体であるが、高温では半導体としての性質をもつ。 共有結晶の代表的な例としてはダイヤモンドやシリコン Si などがある。 ダイヤモンドは、炭素原子 C が共有結合して構成された結晶である。

（イオン結合）
一方の原子が最外殻にある電子を相手の原子に与えて自身は正イオン化し、 電子を受け取った側の原子は負イオン化して、その間の静電引力によって結合が生ずる。 このとき正イオン並びに負イオンはそれぞれ最外殻の軌道が電子で満たされるので安定化する。 一般に金属の塩類はイオン結合により構成される傾向がある。 イオン結合によって構成される固体はイオン結晶と呼ばれる。 イオン結晶は常温において電気の絶縁体であるが、高温では電気伝導性を示す。 更に遷移金属原子 (鉄 Fe やニッケル Ni など) を含むイオン結晶には強磁性を示すものがある。 また イオン結晶が水に溶けると電解質溶液となることが多い。
　[例]　塩化ナトリウム NaCl ，　塩化カリウム KCl　など。

（金属結合）
外側の軌道にあった電子が原子の束縛を離れて原子間を自由に移動し、原子自身は正イオン化すると、 この正イオン化した原子集団と負の移動電子群との間の静電引力によって結合が生ずる。 金属結合によって構成される固体は金属結晶と呼ばれる。 金属結晶は、移動電子群を全原子が共有することになるので、共有結合による巨大分子ともみなせる。 一般に金属結晶は電気や熱の良導体である。
　[例]　ナトリウム Na ， ベリリウム Be ， アルミニウム Al ， 鉄 Fe ， 金 Au　など。

（水素結合）
二つの原子や分子が水素原子を介して弱く結合するとき、それを水素結合という。 水素結合は静電気力が複合的に関与して生ずる。 水素結合の代表的な例としては、氷 H₂O の結晶がある。 また 水素結合は、蛋白質や核酸の高次構造の形成にもかかわっている。

分子の結合エネルギー
分子を単独の原子まで引き離すのに要するエネルギーのことをいう。 例として、水素原子 H 同士の結合エネルギーは 約 435 kJ/mol であり、 炭素原子 C 同士の結合では 約 347 kJ/mol，水素 H と炭素 C の結合では 約 409 kJ/mol などとなる。
［注］ 単位 kJ/mol の呼称は 「キロ ジュール／モル」。
一般に分子の結合エネルギーは、その分子中のすべての結合部分の結合エネルギーの総和に近似的に等しい。

固体の凝集エネルギー
固体のように凝集状態にある原子を互いに引き離すのに要するエネルギーのことをいう。 凝集エネルギーの大きさは、原子間の結合状態によって異なる。 一般に共有結合やイオン結合は凝集エネルギーが大きく、金属結合は比較的小さい傾向がある。 更に水素結合では凝集エネルギーが最も小さい。
　[例]　

結合状態	物質	凝集エネルギー (kJ/mol)
共有結合	シリコン Si	448
イオン結合	塩化ナトリウム NaCl	763
金属結合	ナトリウム Na	108

水素結合の場合の凝集エネルギーの大きさは、およそ 12 kJ/mol から 29 kJ/mol の程度である。

高分子
分子量が 10³ から 10⁶ 程度の非常に大きな分子のことをいう。 高分子物質には、その構成分子が線状に配置するものや 分岐構造をもつもの ならびに 立体的な網状構造をもつもの などがある。 線状や分岐構造をもつ高分子は、加熱すると融解しやすく溶剤等によっても溶けやすいが、 網状構造の高分子は融解し難く、溶剤によっても溶けにくい。 高分子物質を溶媒に溶かして得た溶液が電気伝導性をもつとき、その高分子物質のことを 高分子電解質という。 天然の高分子物質には、多糖類，タンパク質，酵素，核酸 などがある。 また 鉱物性の高分子物質には、雲母や石綿などがある。 人工的に合成された高分子物質には、ポリ塩化ビニル，ポリエチレン，フェノール樹脂など 様々な種類のものがある。

金属
金属結合によって構成される物質の総称であって、水銀 Hg 以外は常温において固体である。 固体金属は、一般に微結晶の集合体であることが多い。 金属の物理的性質としては、電気や熱の良導体であり、展性や延性に富んでいるので 機械的加工が容易である。 一般に金属の電気伝導率は温度上昇とともに減少する。 すなわち 金属の電気抵抗率は温度上昇とともに増大する。 周期表1A族に属するアルカリ金属 (Li，Na，K 等) は、銀白色の光沢を有し、 融点が低く軟らかい性質をもつ。 周期表2A族に属するアルカリ土類金属 (Be，Mg，Ca 等) は、アルカリ金属に比して融点が高い。 遷移元素に属する金属 (Fe，Co，Ni 等) は、強磁性を示し、融点が高く且つ機械的強度も大きい。 金 Au や白金 Pt などの貴金属は、化学的変化を受け難く、美しい光沢を保つ。

半導体
常温における電気伝導率が、金属と絶縁体のほぼ中間の値をもつ物質の総称である。 一般に半導体の電気伝導率は、温度上昇とともに増加する。 すなわち 半導体の電気抵抗率は温度上昇とともに減少する。 絶対零度においては半導体の電気伝導率がほぼ 0 となり、電気伝導性を失う。 シリコン Si やゲルマニウム Ge などは半導体に属する。 半導体には元素の他に、酸化物や有機物並びに高分子など様々な種類のものがある。 概して半導体は、大きな熱起電力を生ずる性質があり、電気伝導率も温度によって 大きく変化する。 ピエゾ半導体と呼ばれる物質は、応力を加えられると電気分極を生ずる。

　原子核 へ進む

　トップページ へ戻る