原子核　atomic nucleus


核 nucleus
原子核は核とも呼ばれ、原子のほぼ中心に位置し、陽子 proton と中性子 neutron が 核力 nuclear force によって強く結合して構成される。 この核力は、微視的(ミクロ)観点から量子論に基づいた考察によると、 中間子 meson と呼ばれる素粒子によって媒介されることが知られている。 ここで素粒子とは、物質を構成する要素の中で最小単位に属する粒子のことをいい、 その大きさは 10⁻¹³ cm 以下のオーダーである。 原子は原子核と電子の間に作用している静電引力によって構成されるが、 この静電気力についても量子論によると光子 photon によって媒介される力であることが知られている。 光子は質量をもたないために、これによって媒介される静電気力は遠方にまで及ぶ。 一方の中間子は質量をもつために、これによって媒介される核力は遠方には及ばない。 核力は核子間に作用する強い短距離力であって、核子間の距離が 10⁻¹³ cm　を超えると急激に減衰する。 したがって 巨視的(マクロ)なレベルにおいては、核力そのものが認識されることはない。 中間子は、電気量をもつもの π^＋，π⁻ と 電気量をもたないもの π⁰ とがある。
［注］ π (パイ)は ギリシャ文字。
π^＋, π⁻ の 質量は 約 2.49×10⁻²⁸ kg ， π⁰ の質量は 約 2.41×10⁻²⁸ kg である。 陽子や中性子のことを総称して核子 nucleon という。 陽子は正電気量 約 1.602×10⁻¹⁹ C (クーロン) をもち、 質量は 約 1.672×10⁻²⁷ kg の素粒子である。 中性子は電気量をもたず、質量 約 1.674×10⁻²⁷ kg の素粒子である。 現在では、陽子 ｐ，中性子 ｎ，中間子 π^＋，π⁻，π⁰ などは、 さらに基本的な粒子であるクォーク quark と呼ばれる粒子から構成されていると考えられている。

核種 nuclide
一般に原子核の種類のことを核種という。 核種の表記方法としては、元素記号を用いて以下のように記す。
　　核種の表記 ：　_Z^A Ｘ
　　Z は陽子 ｐ の個数であり、原子番号に等しい。
　　A は陽子 ｐ の個数と中性子 ｎ の個数の総和で質量数という。
　　Ｘ は原子核の種類で元素記号を用いて表わす。
［例］　₁¹ Ｈ，　₁²Ｈ， 　 ₂⁴Ｈe， 　₂³Ｈe， 　 ₇¹⁴Ｎ， 　₇¹⁶Ｎ 　など。
中性子の個数を N とすると、質量数 A は
　　　　　A ＝ Z ＋N
である。
陽子 ｐ の個数 Z が等しく、中性子 ｎ の個数 N が異なる核のことを 同位核 isotope という。
［例］　₁¹Ｈ　と　₁²Ｈ， 　　　 　₆¹²Ｃ　と　₆¹⁴C ， 　　　　₉₂²³⁵Ｕ　と　₉₂²³⁸Ｕ　など。
陽子 ｐ の個数と中性子 ｎ の個数の総和 A は等しいが、陽子の個数 Z や 中性子の個数 N が異なっている核のことを 同重核 isobar という。
［例］　₄¹⁰Ｂe ，　₅¹⁰Ｂ　など。

原子核の形状
原子核の大きさは およそ 10⁻¹² cm (原子の大きさの 1／10⁴　程度) で、 密度はおよそ 10¹⁴ g・cm⁻³ (比重 10¹⁴) という高密度である。 多くの核は、ほぼ球形とみなせる。核の半径 R は近似的に次式で与えられる。
　　　　R ＝ r A ^1／３　　(ただし　r ＝ 1.3×10⁻¹³cm )
ここで　A は核の質量数である。 この近似式は軽い核については成り立たない。

［例題１］
パラジウム核 ₄₆¹⁰⁶Ｐd の半径は幾 cm か。
（解）
　R ＝ r A ^1／３　より
　R ＝ 1.3×10⁻¹³×(106)^1／3 　cm
　　≒　6.2×10⁻¹³ 　cm

核の結合エネルギーと質量欠損
原子核 _Z^A Ｘ を Z 個の陽子と N 個の 中性子に完全に分解するのに要する仕事は、核が構成されるときに放出されるエネルギーに等しい。 核を作るとき放出されるエネルギーを核の結合エネルギーという。 これが正で大きい程、核は安定である。 一般に核 _Z^A Ｘ の質量 m _Ｘ は、 これを構成する Z 個の陽子 (質量m_ｐ) と N 個の中性子 (質量m_ｎ) の質量の 総和
　Z m_ｐ＋N m_ｎ
よりは小さい。 この質量差 △m は質量欠損と呼ばれ、次式によって与えられる。
　　　△m ＝　Z m_ｐ＋N m_ｎ−m _Ｘ

［例題2］
炭素原子核 ₆¹²Ｃ の質量を 19.92636×10⁻²⁴ g とするとき、 この核の質量欠損は陽子質量の幾 ％ に相当するか。 ただし 陽子，中性子の質量をそれぞれ 1.67262×10⁻²⁴ g ， 1.67493×10⁻²⁴ g とする。
（解）
　△m　＝　Z m_ｐ＋N m_ｎ−m _Ｘ
　　　　＝　6×1.67262×10⁻²⁴g ＋ 6×1.67493×10⁻²⁴g − 19.92636×10⁻²⁴g
　　　　＝　0.1589×10⁻²⁴g
　よって　[0.1589×10⁻²⁴ g ／(1.67262×10⁻²⁴g) ] ×100 ＝ 9.5 ％

核の結合エネルギー B と質量欠損 △m の 間には次の関係がある。
　　　B ＝ c² △m ＝ c² (Z m_ｐ＋N m_ｎ−m _Ｘ )
ただし c は真空中の光速度であって、 およそ 3.0×10⁸ m・s⁻¹ である。

質量とエネルギーの関係
相対論によると、質量 m の物体が速度 v で 運動しているとき、この物体のエネルギー E は
　　　E ＝ m c² [1−(v ／c)² ]^−1／2
で与えられる。 この式において、物体が静止（ v ＝ 0 ）しているときのエネルギーは
　　　E ＝ m c²
となり、質量とエネルギーの等価性が示される。 この m c² を静止エネルギーという。 したがって物体のもつ相対論的な運動エネルギー K は
　　　K ＝ m c² [1−(v ／c)² ]^−1／2 −m c²
となる。
　

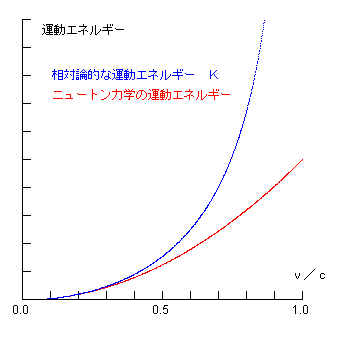
上図において、縦軸は K を m c² でスケールした値 すなわち K／m c² を示す。 なお ニュートン力学の運動エネルギーは　m v²／2　で与えられる。 エネルギーの SI 単位は
　　　J （ジュール）＝ kg・m²・s⁻²
である。

エネルギーの単位 eV
原子や原子核の分野では、エネルギーの単位として eV (エレクトロンボルト) を用いることが多い。 エネルギー 1eV は、電子が 1V (ボルト) の電圧で加速されたときに得るエネルギーである。 エネルギーの単位 eV と J (ジュール) の関係は次のようにして求められる。 電子の電気量の絶対値の大きさは およそ 1.6×10⁻¹⁹ C (クーロン) であるから、 電磁気学の公式
　　　電子の得るエネルギー ＝ 電子の電荷 × 電圧
を用いて
　　　1eV ≒ 1.6×10⁻¹⁹ J (ジュール)
となる。
なお 次のような単位 keV，MeV，GeV などもしばしば用いられる。
　　1 keV ＝ 10³ eV
　　1 MeV ＝ 10³ keV ＝ 10⁶ eV
　　1 GeV ＝ 10³ MeV ＝ 10⁹ eV
　　( k：キロ， 　M：メガ， 　G：ギガ )
原子核や素粒子の分野では、質量の大きさを表わすとき、
　　　eV/c²，　MeV/c²，　GeV/c²
などのように表記することが多い。 ただし c は真空中の光速度である。

［例題３］
質量　0.05 mg を 単位 GeV/c² を用いて表記せよ。 ただし 真空中の光速度 3.0×10⁸ m・s⁻¹， 電子の電気量の絶対値を 1.6×10⁻¹⁹ C とする。
（解）
　E ＝ m c²
　　＝　0.05×10 ⁻⁶ kg ×(3.0×10⁸ m・s⁻¹ )²
　　＝　0.45×10¹⁰ kg・m²・s⁻²
　　＝　0.45×10¹⁰ J
　1 eV ＝ 1.6×10⁻¹⁹ J　　より　
　J ＝ 1／(1.6×10⁻¹⁹ ) eV　　であるから
　E ＝ m c²
　　＝　0.45×10¹⁰×1／(1.6×10⁻¹⁹ ) eV
　　＝　0.28×10²⁹ eV
　　＝　0.28×10²⁹×10⁻⁹ GeV　
　　＝　2.8×10¹⁹ GeV　
　よって　m ＝ 2.8×10¹⁹ GeV /c²

［例題４］
静止していた電子を電圧 20 kV でもって加速したとき、この電子の得る速度を求めよ。 ただし 電子の静止質量を 0.51 MeV/ｃ ² とし、 真空中の光速度を 3.0×10⁸ m・s⁻¹ とする。
（解）
　K ＝ m c² [1−(ｖ ／ｃ)² ]^−1／2 − m c²　　より
　20×10³eV ＝ 0.51×10⁶eV × [1−(ｖ／3.0×10⁸ ｍ・s⁻¹ )² ]^−1／2 − 0.51×10⁶ eV
　よって　v ＝　8.16×10⁷ m・s⁻¹

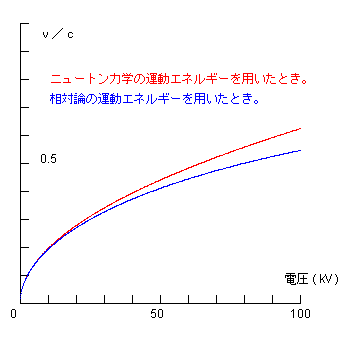
電子を加速する電圧と電子の得る速度比 v ／c　との関係をグラフに示すと下図のようになる。 ただし c は真空中の光速度である。
　

［例題５］
酸素原子核 ₈¹⁶Ｏ の質量を 26.56005×10⁻²⁷ kg とするとき、 この核の結合エネルギーは幾 MeV か。 ただし 陽子，中性子の質量をそれぞれ 1.67262×10⁻²⁷ kg， 1.67493×10⁻²⁷ kg 　とする。 また 真空中の光速度を 3.0×10⁸ m・s⁻¹ 　とし、eV ＝1.6×10⁻¹⁹J 　とする。
（解）
　B ＝ (Z m_ｐ＋N m_ｎ−m_Ｘ ) c²　　より
　B ＝ (8×1.67262×10⁻²⁷ kg ＋ 8×1.67493×10⁻²⁷ kg − 26.56005×10⁻²⁷ kg ) × (3.0×10⁸ m・s⁻¹ )²
　　＝ 1.98315×10⁻¹¹ kg・m²・s⁻²
　　＝ 1.98315×10⁻¹¹ Ｊ
　　＝ 1.98315×10⁻¹¹／(1.6×10⁻¹⁹ ) 　eV
　　＝ 1.24×10⁸ eV
　　＝ 1.24×10⁸×10⁻⁶ MeV
　　＝ 124 MeV


核の結合の強さ
核子１個あたりの結合エネルギー
　　　b ＝ B ／A
は、その核の結合の強さ すなわち 核の安定度を示す尺度である。
軽い核 (質量数 A ≦ 20 ) のとき、b は約 3〜8 MeV であり、 A が 4 の倍数であると特に大きくなる。 これは ₂⁴Ｈ 核 すなわち α (アルファ)粒子が 特に 大きな結合エネルギーをもって安定であるから、 軽い核内においては 2 個の陽子と 2 個の中性子が α 粒子的な集団を作り易いことを意味する。 質量数 20 ≦ A ≦ 190 の核では、b は およそ 8 MeV の値をもつが、 A ＞ 190 のような重い核の b は 7 MeV 程度に減少する。 したがって A が中程度の値のとき b が最も大きくなり、核は安定となる。 天然に存在する 287 種類の安定核を、陽子数 Z や中性子数 N が偶数か奇数か に応じて分類したとき、核の存在数は Z，N とも偶数の場合が最も多く、 Z，N がともに奇数の場合が最も少ない。 このことは 陽子数と中性子数がともに偶数のとき、 核は最も安定であることを示す。 軽い安定核では陽子数 Z と中性子数 N はほぼ等しいが、重い核になるにつれて、 中性子数 N が陽子数 Z より大きくなる。 これを 中性子過剰 neutron excess といい、過剰中性子数　D ＝ N−Z　に対し、 次の経験式が成り立つ。
　　　D ＝ N−Z ≒ 0.006 Z ^5／3
重い核では中性子過剰のとき核が安定である理由は以下のように説明される。 正電気をもつ陽子間には静電気による反発力が作用するために、 陽子数 Z が大きいと核力による結合が弱められて核が不安定となる。 ところが 電気をもたない中性子が多いと核力の寄与が強くなるので、 重い核では中性子過剰のとき核は安定となる。
［例題６］
質量数 195 の白金の核について、過剰中性子数を求めよ。
（解）
　D ＝ N−Z ≒ 0.006 A ^5／3 　より
　D ＝ 0.006×(195)^5／3≒　39

放射性崩壊 radioactive decay
核 Ｘ が放射線を射出して他の核 Ｙ に変換する現象のこと放射性崩壊という。 このとき核 Ｘ を母核、核 Ｙ を娘核という。 放射能 radioactivity とは、放射性の核種に関して放射線を射出する性質のことをいう。 歴史的には、放射能は 1896年に A．H．Becquerel (ベクレル)が ウラン鉱石の放射性を発見したことに始まる。 放射線には、α (アルファ)線，β (ベータ)線，γ (ガンマ)線 の三種類がある。 射出する放射線の種類により α 崩壊，β 崩壊，γ 崩壊 に分類される。 α 線は、高速のヘリウム核 ₂⁴Ｈe (α 粒子) である。 β 線は、高速の電子ｅ⁻や陽電子ｅ^＋から成る。 ここで陽電子ｅ^＋とは、電子ｅ⁻の反粒子であって、 質量は電子と等しいが、電気量については反対の正電気をもつ。 （電子のような素粒子では、必ずその反粒子が存在する。）
γ 線は短波長の電磁波 (光子) である。 α 線のエネルギーは最大でおよそ 9 MeV で、大気中での飛程は 約 10 cm である。 β 線の最高エネルギーは 数 MeV 程度で、アルミニウム金属中の最大飛程は数 mm 程度である。 γ 線は物質に対する透過力が極めて強い。 一般に波長が 10⁻⁸ cm 以下の電磁波を γ 線ということが多いが、 短波長の Ｘ線との区別は明確ではない。
母核 Ｘ のもつ静止エネルギーが娘核 Ｙ および放射線のもつ エネルギーの和よりも大きいとき、母核は自発的に崩壊する可能性をもつ。 放射性核は、放射線を射出して他の種類の核に変換していき、 最終的には安定な非放射性の核となる。 放射能強度は、放射性核の個数が多いほど強いと考えられるので、 放射性崩壊により安定な非放射性核が増加してくると、 一般に放射能強度は時間とともに減衰すると考えられる。 そこで放射性核の個数の時間依存性について求める。 膨大な数の放射性核があるとき、時刻 t に存在する崩壊性核の個数を N， 単位時間あたりに核が崩壊する確率 すなわち崩壊定数を λ (ラムダ) とすると、 微小時間 dt の間に崩壊する核の個数 dN は
　　　dN ＝ −λN dt
である。 すなわち
　　　dN ／dt ＝ −λN
となる。 したがって
　　　dN ／N ＝ −λ dt
積分すると
　　　∫N⁻¹ dN ＝ −λ∫dt ＋ c　　　（ただし c は積分定数）
　　　log_e N ＝ −λt＋c　　　（ただし e は 自然対数の底）
　　　N ＝ e^−λt ＋ c
　　　　 ＝ e^−λt e ^c
　　　　 ＝ Ce^−λt　　　（ここで C ＝ e^c　とした。）
そこで初めの時刻　t ＝ 0　のとき　N ＝ N₀　とすると
　　　C ＝ N₀
よって
　　　N ＝ N₀e^−λt
を得る。 この式は核崩壊の法則を与える。 すなわち 放射性核の個数は、時間とともに指数関数的に減少していく。
　
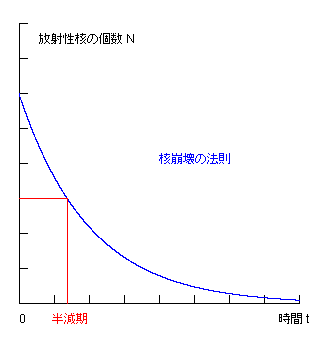
上図においては 横軸ならびに縦軸とも任意スケールであって、全体の傾向のみを示す。
放射性核の平均寿命 τ (タウ) とは、放射性核の個数が現在の数の 1／e に減少する時間である。 核崩壊の法則において、
　　　N ／N₀ ＝ 1／e
として時間を求めると、平均寿命 τ が得られ、
　　　τ ＝ 1／λ
となる。
放射性核の個数が、現在の数の 1／2 に減少するまでの時間Tを 半減期 (half-life) という。 核崩壊の法則において、
　　　N ／N₀ ＝ 1／2
として時間を求めると、半減期 T が得られ、
　　　T ＝ log_e 2／λ ＝ τ log_e 2
となる。
一般に放射能の強さは、単位時間に崩壊する核の個数で表わされる。 単位は１s (秒)間に崩壊する核の個数が１個のとき１Bq (ベクレル) と決める。 放射線が物質中を通過する際に吸収される度合のことを吸収線量という。 その単位は、物質の質量１kg 当たりに吸収される放射線のエネルギーが １J (ジュール) のとき１Gy (グレイ) と決める。 なお 線量当量は、放射線の生物学的効果を考慮した量であって、吸収線量と修正係数の積で定義される。 修正係数は放射線の種類等により異なる。 単位は、吸収線量が Gy (グレイ) のとき、線量当量は Sv (シーベルト) となる。
［例題７］
崩壊定数　1.15×10⁻⁸　s⁻¹　の放射性核が、初めの時刻のときの個数の 1／100　になるまで幾年 (y) かかるか。
（解）
　N ＝ N₀e^−λt　　より
　t ＝−λ⁻¹log_e(N ／N₀)
　t ＝ −(1.15×10⁻⁸ s⁻¹ ) ⁻¹ log_ｅ(1／100)
　　＝ 4.00×10⁸ s
　ここで　1 y (年) ＝ 365×24×60×60 s　　より
　s ＝ 1／(365×24×60×60)　 y (年)　　であるから
　　＝ 4.00×10⁸ ×1／(365×24×60×60) 　y
　　＝12.7 y

［例題８］
半減期 3.05 分の放射性核について、崩壊定数 λ と平均寿命 τ を求めよ。
（解）
　T ＝ log_e 2／λ ＝ τ log_e 2　　より
　λ ＝ log_e 2／T
　　＝ 0.693／(3.05×60 s)
　　＝ 3.79×10⁻³ s⁻¹
　τ ＝ T ／log_e 2
　　＝ (3.05×60 s)／0.693
　　＝ 264 s (秒)

［例題９］
半減期 138 day (日) の放射性核が、初めの時刻のときの個数の 1／1000 になるまで幾年 (y) かかるか。
（解）
　λ ＝ log_e 2 ／T
　　( 1y ＝ 365 day　より　day ＝ 365⁻¹ y )
　　＝ 0.693／(138 day )
　　＝ 0.693／(138×365⁻¹ y )
　　＝ 1.83 y⁻¹
　t ＝ −λ⁻¹ log_e(N ／N₀)
　　＝ −(1.83 y⁻¹) ⁻¹ log_e (1／1000)
　　＝ 3.77 y


崩壊系列
放射性崩壊により母核から生じた娘核は、さらに崩壊して他の核種に変換し、 順次このような変換を続けて最後には非放射性核種に達して安定となる。 これを崩壊系列（放射性系列）といい、次の４種類の系列がある。
　　Ｕ-Ｒa （ウラン-ラジウム）系列：　₉₂²³⁸Ｕ から始まり ₈₂²⁰⁶Ｐb に終わる。
　　Ｔh （トリウム）系列：　　　　　₉₀²³²Ｔh から始まり ₈₂²⁰⁸Ｐb に終わる。
　　Ａc （アクチニウム）系列：　　　　₉₂²³⁵Ｕから始まり ₈₂²⁰⁷Ｐb に終わる。
　　Ｎp （ネプツニウム）系列：　　　₉₃²³⁷Ｎp から始まり ₈₃²⁰⁹Ｂi に終わる。
それぞれの崩壊系列の各段階において、α 崩壊，β 崩壊，γ 崩壊 の ３種類の崩壊様式を伴う。 α 崩壊では、核が α 線 (₂⁴Ｈe) を放出して、 陽子数 Z が 2，中性子数 N が 2 少ない核に変換する。 核 Ｘ がα崩壊
　　_Z^AＸ →　 _Z−2^A−4Ｙ ＋ α
を起こすことができるための条件は、次式が成り立つことである。
　　△m ＝ M_Ｘ−M_Ｙ−M_α ≧ 0
ただし M_Ｘ，M_Ｙ，M_α は、 それぞれ 母核 Ｘ ，娘核 Ｙ，α 粒子 の質量である。 このとき
　　E ＝ c² △m
を崩壊エネルギーといい、その大部分は放出される α 粒子の運動エネルギー となる。 このとき α 粒子の飛程 R は次式で与えられる。
　　　R ＝ C E ^3／2　　(C は定数)

［例題１０］
α 粒子の運動エネルギー E が　9.69 MeV のとき、ある気体中の飛程が 100 mm であった。 E が 4.18 MeV のとき、この気体中での飛程を求めよ。
（解）
　R ＝ C E ^3／2　　より
　100 mm ＝ C (9.69 MeV )^3／2
　R ＝ C (4.18 MeV )^3／2
　したがって
　R ＝ 100 mm ×(4.18MeV／9.69MeV )^3／2
　　＝ 28.3 mm

一つの崩壊系列において、α 粒子の飛程 R と崩壊定数 λ の間には次の関係式が 近似的に成り立つ。
　　　log_e λ ＝ A＋B log_e R
ただし A ，B は各崩壊系列に対して固有の値をとる定数である。 この関係式を Geiger - Nuttal (ガイガー ヌッタル)の法則という。 この式を α 粒子の運動エネルギー E と半減期 T の間の関係式に変形すると、
　　T ＝ T₀ e^{d ／√E}　　　(ただし　T₀ , d　は定数)
となる。 Ｕ-Ｒa 系列については、T₀ ＝ 7.996×10⁻⁶⁴ s ， 　d ＝ 378.7 MeV^1／2 　である。
β 崩壊では、核が β 線 (電子ｅ⁻ または 陽電子ｅ^＋) を放出して、 質量数 A は等しいが陽子数 Z が １ だけ異なる核に変換することをいい、 次の反応式で示されるように、２種類のものがある。
　　β⁻崩壊　： 　_Z^A Ｘ　→　 _Z＋1^A Ｙ ＋ ｅ⁻ ＋ ^-ν_ｅ
　　β^＋崩壊　： 　_Z^A Ｘ　→　 _Z−1^A Ｙ ＋ ｅ^＋ ＋ ν_ｅ
β 崩壊では、β 線の他に電子型ニュートリノ ν_ｅ や 反電子型ニュートリノ ^-ν_ｅ　を放出する。 核内の素過程としては、陽子 ｐ と中性子 ｎ が次式のように相互転換するとき β 崩壊が起こる。
　　β⁻崩壊　：　ｎ →　ｐ ＋ ｅ⁻ ＋ ^-ν_ｅ
　　β^＋崩壊　：　ｐ →　ｎ ＋ ｅ^＋ ＋ ν_ｅ
β 崩壊の際に放出される電子等の運動エネルギーは一定でなく、連続的な値をとり得る。 電子型ニュートリノ ν_ｅ は素粒子の一種であって、電荷をもたない。 ν_ｅ は他の素粒子とは弱く相互作用するだけで、あらゆる物質を貫通する。 電子型ニュートリノの質量は零とみられていたが、現在では極めて小さい質量をもつと考えられている。 α 崩壊は核反応の一種であるが、β 崩壊は弱い相互作用に起因する素粒子反応である。
γ (ガンマ)崩壊では、核が高いエネルギー準位の状態から低いエネルギー準位の状態へ遷移する際に γ 線 (光子) を放出する。 高いエネルギー準位 E_２ の核が 低いエネルギー準位 E_１ に遷移したとき放出される γ 線の 光子のエネルギー E は次式で与えられる。
　　　E ＝ E_２− E_１
一般に α 崩壊や β 崩壊で生成された核は励起状態 (高いエネルギー準位) にあり、 それがさらに γ 線を放出して安定な基底状態 (最低エネルギー準位) に移行することが多い。 γ 崩壊のとき放射される γ 線の振動数 ν は次式で与えられる。
　　　ν ＝ （E_２−E_１ ）／h
ただし h は Planck（プランク）定数と呼ばれる基本定数であって
　　　h ≒ 6.626×10⁻³⁴ J・s
である。

粒子性と波動性
量子論によると、一般に粒子は波動的性質をもつことが知られている。 粒子の運動量やエネルギーは、その粒子の波動的性質を表わすところの波長や振動数に密接に関係している。 光子の場合、そのエネルギー E と光波の振動数 ν の間には
　　　E ＝ h ν
の関係がある。 一般に波の振動数を ν ，波長を λ とすると、波の速度 c は
　　　c ＝ ν λ
で与えられるので、光速度を c とするとき、光子のエネルギーは
　　　E ＝ h c ／λ
のように表せる。 電子の場合は、その運動量 p とすると電子波の波長 λ の間には
　　　p ＝ h／λ
の関係がある。

［例題１１］
励起状態の核が γ (ガンマ)崩壊により、エネルギー 1.08 MeV の γ 線を放出したとき、この γ 線の波長を求めよ。 ただし 真空中の光速度を　3.00×10⁸ m・s⁻¹ とし、 Planck 定数を　6.626×10⁻³⁴ J・s　とする。 また　eV ＝ 1.6×10⁻¹⁹ J　とする。
（解）
　E_２−E_１ ＝ 1.08 MeV
　　　　　＝ 1.08×10⁶ eV
　　　　　＝ 1.08×10⁶×1.6×10⁻¹⁹ J
　　　　　＝ 1.73×10⁻¹³ J
　ν ＝ (E_２−E_１ )／h
　　＝ 1.73×10⁻¹³ J ／(6.626×10⁻³⁴ J・s )
　　＝ 0.261×10²¹ s⁻¹
　λ ＝ c ／ν
　　＝ 3.00×10⁸ m・s⁻¹／(0.261×10²¹ s⁻¹ )
　　＝ 11.5×10⁻¹³ m
　　＝ 1.15×10⁻¹⁰ cm

核反応 nuclear reaction
陽子 ｐ や中性子 ｎ 等の粒子を核に衝突させるときに起こる現象のことを核反応という。 核 Ｘ に粒子 ａ が衝突して核 Ｙ と粒子 ｂ，ｃ，・・・　が生ずるときの反応式は、
　　　Ｘ＋ａ　→　Ｙ＋ｂ＋ｃ＋・・・
のように表わす。 ここで Ｘ を標的核， ａ を入射粒子， Ｙ を生成核，　ｂ，ｃ，・・・　を放出粒子という。
［例］　₇¹⁴Ｎ ＋ α　→　₈¹⁷Ｏ ＋ ｐ
　　　　₄⁹Ｂe ＋ α　→　₆¹²Ｃ ＋ ｎ　　など。
標的核 Ｘ ，生成核 Ｙ の質量を それぞれ 　m_Ｘ ，m_Ｙ　とし、 入射粒子 ａ や放出粒子 ｂ，ｃ　などの質量をそれぞれ 　m_ａ ， m_ｂ ， m_ｃ などとするとき、 反応前後の静止エネルギーの差 Q のことを反応の Q値 といい、次式で与えられる。
　　　Q ＝ （ m_Ｘ＋m_ａ ) c² −（ m_Ｙ＋m_ｂ＋m_ｃ＋・・・ ) c²
Q値が正 (Q ＞ 0) のときは発熱反応であって、入射粒子 ａ の運動エネルギーが小さくても反応が起こる。 Q値が負 (Q ＜ 0) のときは吸熱反応であって、入射粒子 ａ の運動エネルギーが、 ある値以上でなければ反応は起こらない。 このとき必要な最小エネルギーのことを、しきいエネルギー という。 重心系においては、しきいエネルギーは Q の大きさにに等しい。 実験室系において、しきいエネルギーは次式で与えられる。
　　　( しきいエネルギー )　＝　−( m_Ｘ＋m_ａ ) Q ／m_Ｘ
ここで 重心系とは、系の重心に固定した座標系のことをいう。 また 実験室系とは、静止した標的核に固定した座標系のことをいう。

［例題１２］
質量　6.65×10⁻²⁴ g　の粒子を質量　15.01×10⁻²⁴ g　の標的核に衝突させたとき、 実験室系における しきいエネルギーが　8.28 MeV　であった。 このとき反応のQ値を求めよ。
（解）
　( しきいエネルギー )　＝　−( m_Ｘ＋m_ａ ) Q ／m_Ｘ　　より
　8.28 MeV ＝ −(15.01＋6.65）×10⁻²⁴ × Q ／(15.01×10⁻²⁴ )
　よって　Q ＝ −5.74　MeV

正電気をもった粒子 (陽子や α 粒子など) を核に衝突させるには、核との間の静電反発力のために 極めて大きなエネルギーを必要とする。 ところが電気をもたない中性子を核に衝突させる場合には、静電反発力に妨げられることが無く、 低エネルギー (低速) の中性子であっても核反応を起こす。 低速度の中性子は、核の近傍にいる時間が長くなるので核に捕獲されて核反応を起こしやすい。 このような低速度の中性子を 熱中性子 という。 核子１個あたりの結合エネルギーは、中程度の質量数の核が最も大きく約 8.6 MeV であるが、 質量数の大きな非常に重い核では 7.7 MeV 程度と小さくなる。 したがって 非常に重い核に中性子等が衝突すると、ほぼ同質量の中程度の質量数の核に分裂しやすい。 この現象を 核分裂 という。 １個の重い核の分裂により、非常に大きなエネルギーが放出される。 (およそ 200 MeV )
［例］　核分裂する核種　：　　₉₀²²⁷Ｔh， ₉₂²³⁵Ｕ， ₉₂²³⁸Ｕ， ₉₄²³⁹Ｐu　など．
軽い核の核子１個あたりの結合エネルギーは、質量数が中程度の核に比べて小さいために、 軽い核は融合して中程度の質量の核に近づこうとする。 この現象を核融合という。核融合の際に大きなエネルギーが放出される。
［例］　₁²Ｈ ＋ ₁²Ｈ　→　₁³Ｈ ＋ ｐ　　(Q ＝ 4.02 MeV )
　　　　₁²Ｈ ＋ ₁³Ｈ　→　₂⁴Ｈe ＋ ｎ　　(Q ＝ 17.59 MeV )　など．


［補遺］ 前述の各例題を、コンピューターにより計算する際のプログラム言語 JavaScript の記述例

　　　　　JavaScriptを用いた例題の解法へ進む。



　素粒子 へ進む

　トップページ へ戻る